Q. In an L-R circuit $ L=\frac{0.4}{\pi } $ and $R = 30 \, \Omega $ If the circuit has an alternating emf of $220 \,V$ at $50$ cycle/s, the impedance and current in the circuit will be respectively :
Delhi UMET/DPMTDelhi UMET/DPMT 2003
Solution:
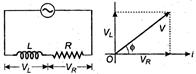
In an L- R circuit, $V_R$ and $V_L$, are mutually perpendicular to each other,
hence impedence $Z = \sqrt{R^2 + X^2_L}$
$\therefore Z = \sqrt{R^2 + (\omega L)^2}$
Given, $R = 30\,\Omega, \omega = 2\pi n$
$ = 2\pi \times 50, L = \frac{0.4}{\pi}$
$\therefore Z = \sqrt{(30)^2 + \left(\frac{2\pi \times 50 \times 0.4}{\pi}\right)^2} = 50\,\Omega$
Current in the circuit is given by
$i = \frac{V}{2} = \frac{220}{50} = 4.4\,A$