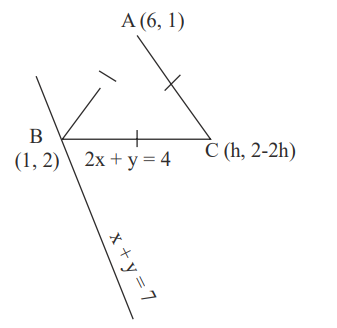Question

In an isosceles triangle $ABC$, the vertex $A$ is $(6,1)$ and the equation of the base $BC$ is $2 x + y =4$. Let the point $B$ lie on the line $x+3 y=7$. If $(\alpha, \beta)$ is the centroid $\triangle A B C$, then $15(\alpha+\beta)$ is equal to :

• A. 39
• B. 41
• C. 51
• D. 63

Answer 1

Answer: (C)

Point B $(1,2)$
Now let $C$ be (h, 4 - 2h)
(As $C$ lies on $2 x + y =4$ )
$\because \Delta$ is isosceles with base $BC$
$\therefore A B=A C$
$\sqrt{25+1}=\sqrt{(6-h)^{2}+(2 h-3)^{2}}$
$\sqrt{26}=\sqrt{36+h^{2}-12 h+4 h^{2}+9-12 h}$
$26=5 h^{2}-24 h+45$
$\Rightarrow 5 h^{2}-24 h+19=0$
$\Rightarrow 5 h^{2}-5 h-19 h+19=0$
$h=\frac{19}{5}$ or $h =1$
Thus $C\left(\frac{19}{5}, \frac{-18}{5}\right)$
Centroid $\left(\frac{6+1+\frac{19}{5}}{3}, \frac{1+2-\frac{18}{5}}{3}\right)$
$\left(\frac{35+19}{15}, \frac{15-18}{15}\right)$
$\left(\frac{54}{15}, \frac{-3}{15}\right)$
$\alpha=\frac{54}{15} ; \beta=\frac{-3}{15}$
$15(\alpha+\beta)=51$