Q.
In an interference arrangement similar to Young's
double-slit experiment, the slits $S_1$, and $S_2$ are illuminated
with coherent microwave sources, each of frequency $10^6$ Hz.
The sources are synchronized to have zero phase
difference. The slits are separated by a distance d = 150.0 m.
The intensity I$(\theta)$ is measured as a function of $\theta$, where $\theta$ is
defined as shown. If $I_0$ is the maximum intensity, then I$(\theta)$
for $0 \le \theta \le$90$^{\circ}$ is given by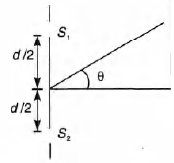
IIT JEEIIT JEE 1995
Solution: