Q. In an experiment, a small steel ball falls through a liquid at a constant speed of $10\, cm/s$. If the steel ball is pulled upward with a force equal to twice its effective weight, how fast will it move upward ?
Solution:
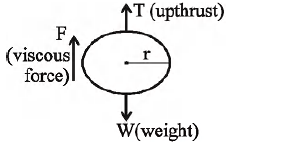
Weight of the body
$W=mg=\frac{4}{3} \pi r^{3} \rho g$
$T=\frac{4}{3} \pi r^{3} \sigma g$
andF =$6\pi\eta vr $
When the body attains terminal velocity net force acting on the body is zero, i.e.,
$W-T-F=0$
And terminal velocity $v=\frac{2}{9}\frac{r ^{2}\left(\rho-\sigma\right)g}{\eta}$
As in case of upward motion upward force is twice its effective weight, therefore, it will move with same speed $10\, cm/s$