Q.
In a Young's double slit experiment, the slit separation d is 0.3 mm and the screen distance D is 1m. A parallel beam of light of wavelength 600nm is incident on the slits at angle α as shown in figure. On the screen, the point O is equidistant from the slits and distance PO is 11.0 mm. Which of the following statement(s) is/are correct ?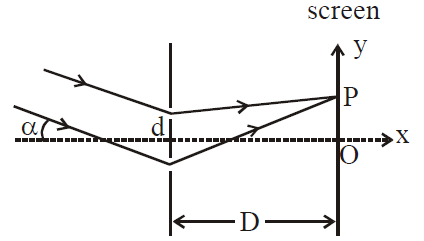
Solution: