Q.
In a YDSE, the light of wavelength $I=5000\,\mathring{A}$ is used, which emerges in phase from two slits a distance $d=3 \times 10^{-7} m$ apart. A transparent sheet of thickness $t=1.5 \times 10^{-7} m$ refractive index $\mu=1.17$ is placed over one of the slits. what is the new angular position of the central maxima of the interference pattern, from the center of the screen? Find the value of $y$.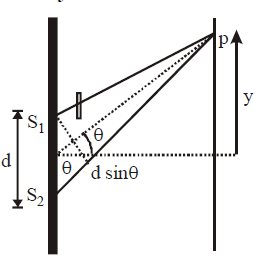
BITSATBITSAT 2015
Solution: