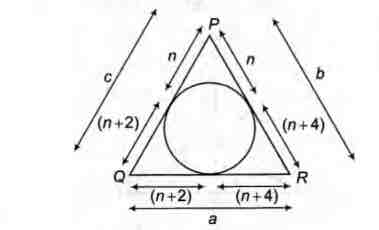
Q.
In a $\triangle$ PQR, P is the largest angle and cos P = $ \frac{1}{3}$.
Further in circle of the triangle touches the sides
PQ,QR and RP at N ,L and M respectively, such
th a t the lengths of P N , QL and RM a re consecutive
even integers. Then, possible length(s) of the side(s)
of the triangle is (are)
Solution:
PLAN Whenever cosine of angle and sides are given or to find out, we
should always use Cosine law.
i,e., cos A = $ \frac{b^2 + c^2 - a^2 }{ 2bc} , \, cos \, B = \frac{a^2 + c^2 - b^2 }{2 ac}$
and cos C = $ \frac{a^2 + b^2 - c^2 }{ 2ab}$
$\therefore cos \, P = \frac{ b^2 + c^2 - a^2 }{ 2 bc }$
$\Rightarrow \frac{1}{3} = \frac{(2 n + 4 )^2 + (2n + 2)^2 - (2n + 6 )^2 }{ 2 (2n + 4) \, (2n + 2)} $
$$ $\bigg [ \because \, cos \, p = \frac{1}{3}, \, given \bigg ] $
$\Rightarrow \frac{ 4n^2 - 16 }{ 8 ( n + 1) \, (n + 2) } = \frac{1}{3}$
$\Rightarrow \frac{ n^2 - 4 }{ 2 (n + 1) \, (n + 2)} = \frac{1}{3}$
$\Rightarrow \frac{( n - 2) }{ 2 \, (n + 1) } \frac{1}{3}$
$\Rightarrow 3 n - 6 = 2n + 2 \Rightarrow n = 8 $.
$\therefore $ Sides are (2n + 2), (2n + 4), (2n + 6), i.e, 18,20,22