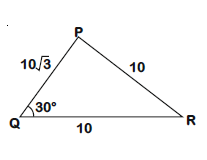
Question

In a triangle $PQR$, let $\angle 𝑃𝑄𝑅 = 30^{\circ}$ and the sides $PQ$ and $QR$ have lengths $10 \sqrt{3}$ and 10, respectively. Then, which of the following statement(s) is (are) TRUE?

• A. $\angle QPR = 45^{\circ} $
• B. The area of the triangle $PQR$ is $25 \sqrt{3}$ and $\angle QPR = 120^{\circ} $
• C. The radius of the incircle of the triangle $PQR $ is $10 \sqrt{3} - 15$
• D. The area of the circumcircle of the triangle $PQR$ is $100 \, \pi $

Answer 1

Answer: (B), (C), (D)

$\cos30^{\circ}= \frac{\left(10\sqrt{3}\right)^{2} + 10^{2} - PR^{2}}{2\left(10\sqrt{3}\right)\left(10\right)} $
$\Rightarrow PR = 10$
$ \angle QPR = 30^{\circ}$
Area of triangle PQR $= \frac{1}{2} (10)(10\sqrt{3})(\sin 30^{\circ})$
$ = 25 \sqrt{3}$
Also, $r = \frac{\Delta}{s} = \frac{25 \sqrt{3}}{10 + 5 \sqrt{3}}$
$ = 5 \sqrt{3} (2 - \sqrt{3} ) = 10 \sqrt{3} - 15 $
$R = \frac{abc}{4\Delta} = \frac{(10)(10)(10 \sqrt{3})}{4(25 \sqrt{3})} = 10 $
Area of the circumcircle $ = \pi (10)^2 = 100 \pi $