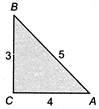
Q. In a triangle $ABC$, if $ a=3,b=4,c=5, $ then the distance between its incentre and circumcentre is
Solution:
Given, $ a=3,b=4,c=5 $
$ \Rightarrow $ $ {{c}^{2}}={{a}^{2}}+{{b}^{2}} $
Therefore, it is a right angled triangle at C.
$ \therefore $ $ R=\frac{1}{2}c=\frac{5}{2} $ and $ r=\frac{\Delta }{s}=\frac{\frac{1}{2}\times 3\times 4}{\frac{12}{2}}=1 $
$ \therefore $ Distance between incentre and circumcentre
$=\sqrt{{{R}^{2}}-2Rr} $
$=\sqrt{{{\left( \frac{5}{2} \right)}^{2}}-2.\frac{5}{2}.1} $
$=\sqrt{\frac{5}{2}}\sqrt{\frac{5}{2}-2}=\frac{\sqrt{5}}{2} $