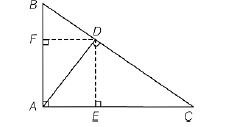
Question

In a triangle $ABC$, $\angle BAC = 90^{\circ}$ ; $AD$ is the altitude from $A$ on to $BC$. Draw $DE$ perpendicular to $AC$ and $DF$ perpendicular to $AB$. Suppose $AB = 15$ and $BC = 25$. Then the length of $EF$ is

• A. $12$
• B. $10$
• C. $5\sqrt{3}$
• D. $5\sqrt{5}$

Answer 1

Answer: (A)

It is given that in triangle $ABC$

$\angle BAC=90^{\circ}, AD$ is the altitude from A on to BC



Since, $AB = 15$ and $BC = 25$

$\therefore AC=\sqrt{BC^{2}-AB^{2}}=\sqrt{625-225}$

$=\sqrt{400}=20$

Now, since area of $ \Delta ABC =\frac{1}{2} \left(BC\right)\left(AD\right)$

$=\frac{1}{2}\left(AB\right)\left(AC\right)$

$\Rightarrow \frac{1}{2}\left(BC\right)\left(AD\right)$

$=\frac{1}{2}\times15\times20$

$\Rightarrow 25\times AD=300$

$\Rightarrow AD=12$

$\because AEDF$ is a rectangle, then

$EF=AD=12$