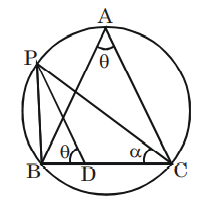
Q. In a triangle $ABC$, a point $D$ is chosen on $BC$ such that $BD : DC =2: 5$. Let $P$ be a point on the circumcircle $A B C$ such that $\angle P D B=\angle B A C$. Then $PD : PC$ is :-
KVPYKVPY 2020
Solution: