Q.
In a thermodynamic process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by T$\Delta$X, where T is temperature of the system and $\Delta$X is the infinitesimal change in a thermodynamic quantity X of the system. For a mole of monatomic ideal gas $X = \frac{3}{2} R\, In \left(\frac{T}{T_{A}}\right)+R\,In \left(\frac{V}{V_{A}}\right)$. Here, R is gas constant, V is volume of gas, $T_{A}$ and $V_{A}$ are constants.
The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.
List-I
List-II
(I) Work done by the system in process 1$\to$2$\to$3
(p) $\frac{1}{3}RT_{0} \,In\,2$
(II) Change in internal energy in process 1$\to$2$\to$3
(Q) $\frac{1}{3}RT_{0}$
(III) Heat absorbed by the system in process 1$\to$2$\to$3
(R) $RT_{0}$
(IV) Heat absorbed by the system in process 1$\to$2
(S) $\frac{4}{3}RT_{0}$
(T) $\frac{1}{3}RT_{0} \left(3+In\,2\right)$
(U) $\frac{5}{6}RT_{0} $
Question: If the process carried out on one mole of monatomic ideal gas is as shown in figure in the PV-diagram with $P_{0} V_{0} = \frac{1}{3}RT_{0},$ the correct match is.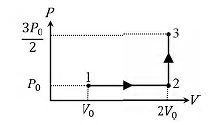
| List-I | List-II |
|---|---|
| (I) Work done by the system in process 1$\to$2$\to$3 | (p) $\frac{1}{3}RT_{0} \,In\,2$ |
| (II) Change in internal energy in process 1$\to$2$\to$3 | (Q) $\frac{1}{3}RT_{0}$ |
| (III) Heat absorbed by the system in process 1$\to$2$\to$3 | (R) $RT_{0}$ |
| (IV) Heat absorbed by the system in process 1$\to$2 | (S) $\frac{4}{3}RT_{0}$ |
| (T) $\frac{1}{3}RT_{0} \left(3+In\,2\right)$ | |
| (U) $\frac{5}{6}RT_{0} $ |
JEE AdvancedJEE Advanced 2019
Solution: