Question

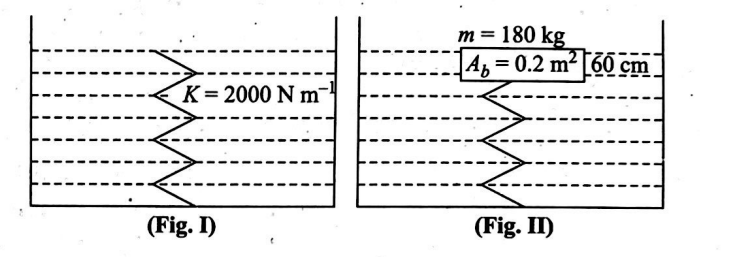
In a tank of horizontal cross-sectional area $1\, m ^{2}$, a spring with force constant $2000\, N\, m ^{-1}$ is fixed in vertical position upto the height of the water as shown in figure I. A block of mass $180\, kg$ is gently placed over the spring and it attains the equilibrium position as shown in figure II. If base area of the block is $0.2 \,m ^{2}$ and height $60 \,cm$, then find compression (in $cm$ ) in the spring in equilibrium position.
(Take $g=10\, m / s ^{2}, \rho_{w}=1000\, kg / m ^{3}$ )

Answer 1

As block goes down by distance $x$, water comes up by distance $y$. As both are measured from initial level of water, compression in the spring is $x$ but the block is in depth $(x+y)$ in water.
Applying conservation of volume

$0.2 \times x=\left(1 m ^{2}-0.2 m ^{2}\right) \times y$
$x=4 y \Rightarrow y=\frac{x}{4}$
Thus, total depth of block in water $=\frac{x}{4}+x=\frac{5 x}{4}$
Free body diagram of the block in equilibrium:
$F_{b}=(0.2)(5 x / 4)(1000)(10)$
For equilibrium,
$m g=k x+F_{B}$

$\Rightarrow 1800=2000 x+(0.2)\left(\frac{5 x}{4}\right)(1000)(10)$
$\Rightarrow 18=20 x+25 \,x $
$\Rightarrow x=\frac{18}{45} m =40\, cm$