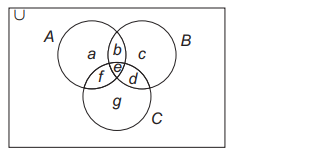
Question

In a survey, it was found that 21 people like product $A$, 26 like product $B$ and 29 like product $C$. If 14 people like products $A$ and $B, 12$ people like products $C$ and $A, 14$ people like products $B$ and $C$ and 8 like all the three products, then number of people who liked product $C$ only, is

• A. 7
• B. 15
• C. 11
• D. 9

Answer 1

Answer: (C)

Let $A$ be the set who like product $A, B$ be the set who like product $B$ and $C$ be the set who like product $C$.

Then,
$n(A) =21, n(B)=26, n(C)=29$
$n(A \cap B) =14, n(B \cap C)=14$
$n(A \cap C) =12, n(A \cap B \cap C)=8$
$a+b+e+f =21 .... $(i)
$b+c+d+e =26....$(ii)
$d+e+f+g =29.....$(iii)
$b+e =14.....$(iv)
$e+d =14 .... $(v)
$f+e =12 ....$(vi)
$e =8....$(vii)
Substituting the values of $e$ in Eqs. (iv), (v) and (vi), we get
$b=6, d=6 $ and $ f=4$
Substituting the values of $d, e$ and $f$ in Eq. (iii), we get
$\therefore 6+8+4+g =29 $
$\therefore g =11$
Number of people who like product $C$ only, is $11 $.
Alternate Method
$n\left(C \cap A^{\prime} \cap B^{\prime}\right) =n(C)-n(C \cap A)-n(C \cap B) $
$ + n(A \cap B \cap C)$
$ =29-12-14+8 $
$ =37-26 $
$ =11$