Q.
In a meter bridge, the wire of length $1\, m$ has a non-uniform cross-section such that, the variation $\frac{dR}{dl}$ of its resistance $R$ with length $l$ is $\frac{dR}{dl} \propto \frac{1}{\sqrt{l}}$. Two equal resistances are connected as shown in the figure. The galvanometer has zero deflection when the jockey is at point $P$. What is the length $AP$ ?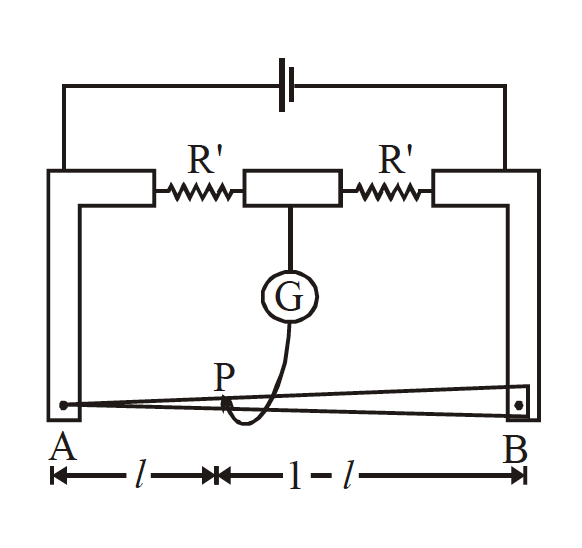
Solution: