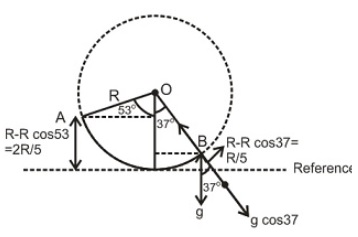
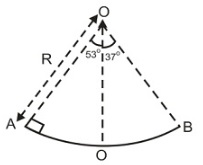
Question

In a fixed quarter circular track of radius $R$ which lies in a vertical plane, a block is released from point $A$ and it leaves the path at point $B$ . The radius of curvature of its trajectory when it just leaves the path will be

• A. $R$
• B. $\frac{\text{R}}{4}$
• C. $\frac{\text{R}}{2}$
• D. None of these

Answer 1

Answer: (C)

By energy conservation between A and B
$⇒ \, \, \, \text{Mg} \frac{2 \text{R}}{5} + 0 = \frac{\text{MgR}}{5} + \frac{1}{2} \text{Mv}^{2}$
$\text{v} = \sqrt{\frac{2 \text{gR}}{5}}$

Now, radius of curvature after just leaving B is
$\text{r} = \frac{\text{v}_{\bot}^{2}}{\text{a}_{\text{r}}} = \frac{2 \text{gR} / 5}{\text{g cos 37}} = \frac{\text{R}}{2}$