Q.
In a cylindrical water tank there are two small holes $Q$ and $P$ on the wall at a depth of $h_{1}$ from the upper level of water and at a height of $h_{2}$ from the lower end of the tank, respectively, as shown in the figure. Water coming out from both the holes strike the ground at the same point. The ratio of $h_{1}$ and $h_{2}$ is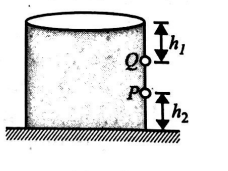
Mechanical Properties of Fluids
Solution:
