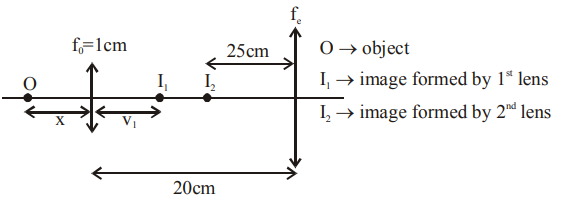
Question

In a compound microscope, the magnified virtual image is formed at a distance of $25 \,cm$ from the eye-piece. The focal length of its objective lens is $1\, cm .$ If the magnification is $100$ and the tube length of the microscope is $20\, cm ,$ then the focal length of the eye-piece lens (in $cm$ ) is __________.

Answer 1

for first lens $=\frac{1}{ v _{1}}-\frac{1}{- x }=\frac{1}{1} \Rightarrow v _{1}=\frac{ x }{ x -1}$
also magnification $\operatorname|{m}_{1}|=| \frac{ v _{1}}{ u _{1}} \mid=\frac{1}{ x -1}$
for $2^{\text {nd }}$ lens this is acting as object
so $u _{2}=-\left(20- v _{1}\right)=-\left(20-\frac{ x }{ x -1}\right)$
and $v _{2}=-25 cm$
angular magnification $|m_{ A }| =\left|\frac{ D }{ u _{2}}\right|=\frac{25}{\left| u _{2}\right|}$
Total magnification $m = m _{1} m _{ A }=100$
$\left(\frac{1}{ x -1}\right)\left(\frac{25}{20-\frac{ x }{ x -1}}\right)=100$
$\frac{25}{20( x -1)- x }=100 $
$\Rightarrow 1=80( x -1)-4 x$
$\Rightarrow 76 x =81 $
$\Rightarrow x =\frac{81}{76}$
$\Rightarrow u _{2}=-\left(20-\frac{81 / 76}{81 / 76-1}\right)=\frac{-19}{5}$
now by lens formula
$\frac{1}{-25}-\frac{1}{-19 / 5}=\frac{1}{ f _{ e }} $
$\Rightarrow f _{ e }=\frac{25 \times 19}{106} \approx 4.48 cm$