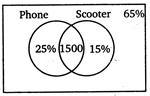
Q. In a certain town $25\%$ families own a cell phone, $15\%$ families own a scooter and $65\%$ families own neither a cell phone nor a scooter. If $1500$ families own both a cell phone and a scooter, then the total number of families in the town is
Solution:
Let the total population of town be $ x $ .
$ \therefore $ $ \frac{25x}{100}+\frac{15x}{100}-1500+\frac{65x}{100}=x $
$ \Rightarrow $ $ \frac{105x}{100}-x=1500 $
$ \Rightarrow $ $ \frac{5x}{100}=1500 $
$ \Rightarrow $ $ x=30000 $