1. Tardigrade
  2. Question
  3. Physics
  4. In a certain region of space, electric field is along the z-direction throughout. The magnitude of electric field is however not constant, but increases uniformly along the positive z-direction at the rate of 105 N C-1 m-1. The force experienced by the system having a total dipole moment equal to 10-7 C m in the negative z- direction is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

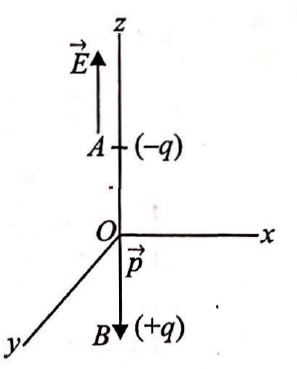
Q. In a certain region of space, electric field is along the $z$-direction throughout. The magnitude of electric field is however not constant, but increases uniformly along the positive $z$-direction at the rate of $10^5\, N\, C^{-1}\, m^{-1}$. The force experienced by the system having a total dipole moment equal to $10^{-7}\, C\, m$ in the negative $z$- direction is

AIIMSAIIMS 2017Electric Charges and Fields

Solution:

Consider an electric dipole with $-q$ charge at $A$ and $+q$ charge at By placed along $z$-axis, that its dipole moment is in negative $z$ direction.
i.e., $p_z = - 10^{-7}\,C\,m$
The electric field is along positive direction of $z$-axis, such that
$\frac{d\text{E}}{dz}=10^{5}\,N\,C^{-1}\,m^{-1}$
From $F= qdE=\left(q\times dz\right)\times\frac{dE}{dz}=p \frac{dE}{dz}$
$\therefore F=-10^{-7}\times10^{5}=-10^{-2}\,N$

Solution Image