Q.
In a certain region, electric and magnetic fields exist as $E\hat{i}$ and $B\hat{k}$ respectively. If a particle having mass $m$ and charge $q$ moves under the influence of these fields, it follows a trajectory from $P$ to $Q$ as indicated in the adjoining figure. If it is known that the velocities at $P$ and $Q$ are $v\hat{i}$ and $-2v\hat{j}$ respectively, then choose the correct statements out of the following.
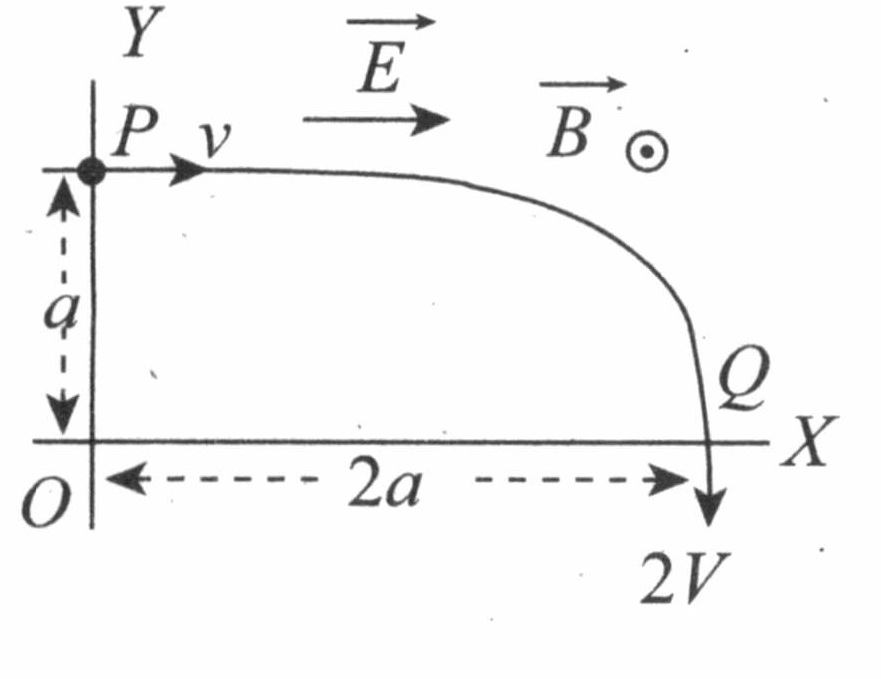
(a) $E=\frac{3}{4}\frac{m v^{2}}{q a}$
(b) $E=\frac{3}{2}\frac{m v^{2}}{q a}$
(c) Rate of work done by magnetic field at any point is zero.
(d) Rate of work done by electric field at any point is zero.
NTA AbhyasNTA Abhyas 2020
Solution:
From work-energy theorem:
Work done by the electric force is equal to the change in kinetic energy.
$W_{F_{E}}=\Delta K.E.$
$\left(\right.qE\left.\right)\left(\right.2a\left.\right)=\frac{1}{2}m\left[\right.\left(2 v\right)^{2}-\left(v\right)^{2}\left]\right.\left[\because W_{F_{E}} = F_{E} \times 2 a\right]$
or $E=\frac{3}{4}\left(\frac{m v^{2}}{q a}\right)$
Rate of work done by magnetic field at any point
$P=\overset{ \rightarrow }{F_{m}}\cdot \overset{ \rightarrow }{v}=0$ as $\overset{ \rightarrow }{\left(\right. F_{m}}\bot\overset{ \rightarrow }{v}\left.\right)$ always.
At P, rate of work done by electric field will be;
$P=\overset{ \rightarrow }{F_{E}}.\overset{ \rightarrow }{v}$
$\Rightarrow P=\left(q E\right)\left(v\right)cos0^\circ $
$\Rightarrow P=q\frac{3}{4}\left(\frac{m v^{2}}{q a}\right)v$
$\Rightarrow P=\frac{3}{4}\frac{m v^{3}}{a}$
At Q, rate of work done by electric field is zero because electric field is perpendicular to the velocity of the particle at point Q.
Work done by the electric force is equal to the change in kinetic energy.
$W_{F_{E}}=\Delta K.E.$
$\left(\right.qE\left.\right)\left(\right.2a\left.\right)=\frac{1}{2}m\left[\right.\left(2 v\right)^{2}-\left(v\right)^{2}\left]\right.\left[\because W_{F_{E}} = F_{E} \times 2 a\right]$
or $E=\frac{3}{4}\left(\frac{m v^{2}}{q a}\right)$
$P=\overset{ \rightarrow }{F_{m}}\cdot \overset{ \rightarrow }{v}=0$ as $\overset{ \rightarrow }{\left(\right. F_{m}}\bot\overset{ \rightarrow }{v}\left.\right)$ always.
At P, rate of work done by electric field will be;
$P=\overset{ \rightarrow }{F_{E}}.\overset{ \rightarrow }{v}$
$\Rightarrow P=\left(q E\right)\left(v\right)cos0^\circ $
$\Rightarrow P=q\frac{3}{4}\left(\frac{m v^{2}}{q a}\right)v$
$\Rightarrow P=\frac{3}{4}\frac{m v^{3}}{a}$
At Q, rate of work done by electric field is zero because electric field is perpendicular to the velocity of the particle at point Q.