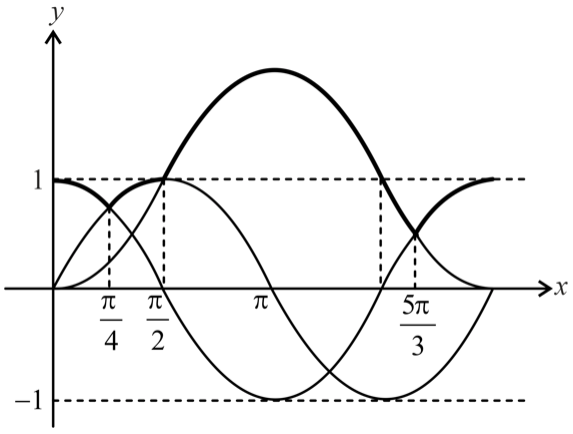
Question

In $\left(\right.0,2\pi \left.\right)$ , the total number of points, where $f\left(x\right)=max\left\{sin x , cos x , 1 - cos x\right\}$ is not differentiable, is

• A. $3$
• B. $4$
• C. $5$
• D. $6$

Answer 1

Answer: (A)

$f\left(x\right)=max\left\{sin x , cos x , 1 - cos x\right\}$
The graph of $f\left(x\right)$ is

$\Rightarrow $ $f\left(x\right)$ is not differentiable at sharp points, which are $x = \frac{\pi }{4} , \, \frac{\pi }{2} , \, \frac{5 \pi }{3}$ .
$\Rightarrow $ $f\left(x\right)$ is not differentiable at $3$ points.