1. Tardigrade
  2. Question
  3. Mathematics
  4. If x+y≤2,x ≥ 0,y ≥ 0 the point at which maximum value of 3x + 2y attained will be

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

Q. If $x+y\leq2,x \geq 0,y \geq 0$ the point at which maximum value of $3x + 2y$ attained will be

KCETKCET 2014Linear Programming

Solution:

Given, $x+y \leq 2, x \geq 0$ and $y \geq 0$
Let $z=3 x+2 y$
Now, table for $x+y=2$
x 0 2 1
y 2 0 1
At $(0,0), 0+0 \leq 2$
$\Rightarrow 0 \leq 2$, which is true.
So, shaded portion is towards the origin.
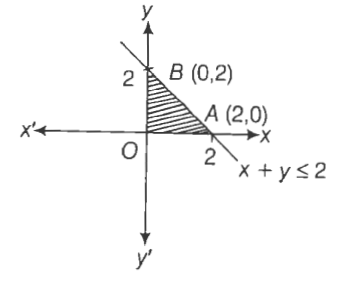
image
$\therefore $ The corner points on shaded region are $O(0,0), A(2,0)$ and $B(0,2)$
At point $O(0,0), z=3(0)+2(0)=0$
At point $A(2,0), z=3(2)+2(0)=6$
At point $B(0,2), z=3(0)+2(2)=4$
Hence, maximum value of $z$ is 6 at point $(2,0)$.