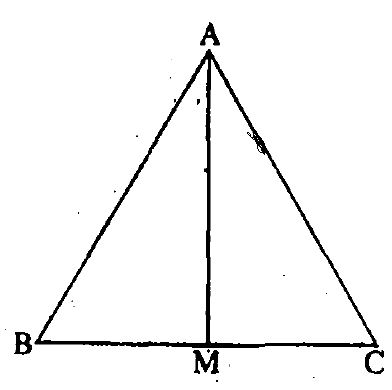
Q. If vectors $\overrightarrow{AB}=3\,\hat{i}-3\,\hat{k}$ and $\overrightarrow{AC}=\hat{i}-2\,\hat{j}+\hat{k}$ are the sides of a triangle ABC, then the length of the median AM, is
Vector Algebra
Solution:
Solution: