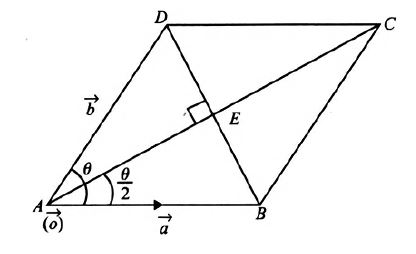
Q. If $\vec{a}$ and $\vec{a}$ are two unit vectors and $\theta$ is the angle between them, then the unit vector along the angular bisector of $\vec{a}$and $\vec{b}$ will be given by
Vector Algebra
Solution:
Solution: