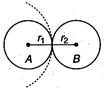
Question

If two soap bubbles of equal radii $r$ coalesce, then the radius of curvature of interface between two bubbles will be

• A. r
• B. zero
• C. infinity
• D. $ \frac{1}{2r} $

Answer 1

Answer: (C)

Let radius of curvature of the common internal film surface of the double bubble formed be $r$.
Then, excess of pressure as compared to atmosphere inside $A$ is
$\frac{4 T}{r_{1}}$ and $B$ is $\frac{4 T}{r_{2}}$.
The pressure difference is
$\frac{4 T}{r_{1}}-\frac{4 T}{r_{2}}=\frac{4 T}{r'} $
$\Rightarrow r'=\frac{r_{1} r_{2}}{r_{2}-r_{1}} $
Given, $r_{1}=r_{2}=r$
$\therefore r'=\frac{r^{2}}{0}=\infty$