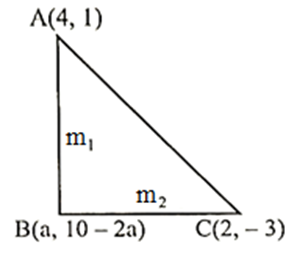
Q. If the vertex opposite to the hypotenuse of a right-angled triangle lies on the straight line $2x+y-10=0$ and the two other vertices are $\left(2 , - 3\right)$ and $\left(4 , 1\right)$ , then the area of the triangle (in sq. units) is equal to
NTA AbhyasNTA Abhyas 2020Straight Lines
Solution: