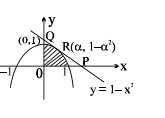Question

If the tangent to the curve $y =1- x ^2$ at $x =\alpha$, where $0< \alpha< 1$, meets the axes at P and Q. Also $\alpha$ varies, the minimum value of the area of the triangle $O P Q$ is $k$ times the area bounded by the axes and the part of the curve for which $0< x <1$, then $k$ is equal to

• A. $ \frac{2}{\sqrt{3}}$
• B. $\frac{75}{16}$
• C. $\frac{25}{18}$
• D. $\frac{2}{3}$

Answer 1

Answer: (A)

$ A _1=$ area under the curve and axes
$=\int\limits_0^1\left(1-x^2\right) d x=\left[x-\frac{x^3}{3}\right]_0^1=\frac{2}{3}$
Now
$\text { Now } y=1-x^2 \therefore y^{\prime}=-2 x $
$\therefore y^{\prime}\left(\alpha, 1-\alpha^2\right)=-2 \alpha$
Equation of tangent to the curve $y=1-x^2$
$\left( y -\left(1-\alpha^2\right)\right)=-2 \alpha( x -\alpha) $
$2 \alpha x + y =\alpha^2+1$
$\therefore P \equiv\left(\frac{\alpha^2+1}{2 \alpha}, 0\right) ; Q \equiv\left(0, \alpha^2+1\right)$
$A =\text { Area of triangle } POQ =\frac{1}{2}( OP )( OQ )=\frac{1}{4} \frac{\left(\alpha^2+1\right)^2}{\alpha} $
$\therefore A ^{\prime} =\frac{1}{4} \frac{\alpha \cdot 2\left(\alpha^2+1\right) 2 \alpha-\left(\alpha^2+1\right)^2}{\alpha^2}=\frac{1}{4} \frac{3 \alpha^4+2 \alpha^2-1}{\alpha^2}$
For maximum $/$ minimum, $A ^{\prime}=0 \Rightarrow 3 \alpha^4+2 \alpha^2-1=0 \Rightarrow \alpha^2=-1, \frac{1}{3} \Rightarrow \alpha= \pm \frac{1}{\sqrt{3}}$
$\therefore 0<\alpha<1 \Rightarrow \alpha=\frac{1}{\sqrt{3}}, A ^{\prime \prime}>0$ hence $A$ is minimum
$A=\frac{1}{4} \frac{\left(\frac{1}{3}+1\right)^2}{\frac{1}{\sqrt{3}}}=\frac{4}{3 \sqrt{3}}$....(ii)
since $A = kA$ (given)
From (i) and (ii) $\frac{4}{3 \sqrt{3}}=k \cdot \frac{2}{3} \Rightarrow k =\frac{2}{\sqrt{3}}$