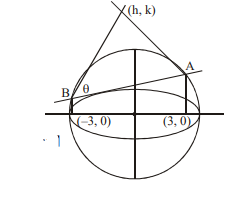
Q. If the tangent drawn to ellipse $\frac{x^2}{25}+\frac{y^2}{16}=1$ intersect the circle $x^2+y^2=25$ at $A$ and $B$, then the locus of the point of intersection of tangents at $A$ and $B$ is
Conic Sections
Solution:
Equation of $AB : xh + yk =25$....(1)
Also, $\frac{x \cos \theta}{5}+\frac{y \sin \theta}{4}=1$.....(2)
$\therefore \frac{\cos \theta}{5 h }=\frac{\sin \theta}{4 k }=\frac{1}{25}$
Use $c^2+s^2=1$
$\Rightarrow \frac{x^2}{25}+\frac{y^2}{\left(\frac{25}{4}\right)^2}=1 $