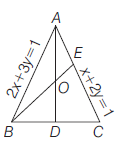
Question

If the straight line $2\, x+3\, y-1=0$ $x+2 \,y-1=0$ and
$a \,x+b \,y-1=0$ form a triangle with origin as orthocentre, then $(a, b)$ is equal to

• A. (6,4)
• B. (-3,3)
• C. (-8,8)
• D. (0,7)

Answer 1

Answer: (C)

The equation of a line through $A$ i.e. the point of intersection of
$A B$ and $A C$ is $(x+2 y-1)+\lambda(2 x+3 y-1)=0$
If it passes through $(0,0)$, then $-1-\lambda=0$
$-1-\lambda =0 $
$ \Rightarrow \lambda =-1 $
On substituting $\lambda=-1$ in Eq. (i),
we get $x+y=0$ as the equation of $A D$. Since, $A D \perp B C$, therefore
$1 \times -\frac{a}{b}=-1 $
$ \Rightarrow a+b=0$......(ii)
Similarly, by applying the condition that $B O$ is perpendicular to $C A$, we get $a+2 b=8$
On solving Eqs. (ii) and (iii), we get
$a=-8, b=8$. ........(iii)
On solving Eqs. (ii) and (iii), we get $a=-8, b=8$.