Question

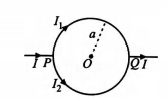
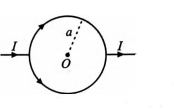
If the resistance of the upper half of a rigid loop is twice that of the lower half, the magnitude of magnetic induction at the centre is equal to

• A. zero
• B. $\frac{\mu_{0} I}{4 a}$
• C. $\frac{\mu_{0} I}{12 a}$
• D. $\frac{\mu_{0} I}{3a}$

Answer 1

Answer: (C)

$\because I_{1} R_{1}=I_{2} R_{2}$
$\frac{I_{1}}{I_{2}}=\frac{R_{2}}{R_{1}}=\frac{R_{2}}{2 R_{2}}=\frac{1}{2}$
$\therefore I_{2}=2 I_{1}$
and $I=I_{1}+I_{2}=I_{1}+2 I_{1}=3 I_{1}$
$ \therefore I_{1}=\frac{I}{3}$ and $I_{2}=\frac{2}{3} I$
Magnetic field at the centre of coil is
$\vec{B}_{O}=B_{1} \otimes+B_{2} \odot$
$\therefore B_{O}=-\frac{\mu_{0} I_{1} \pi}{4 \pi a}+\frac{\mu_{0} I_{2} \pi}{4 \pi a}$
$B_{O}=\frac{\mu_{0} \pi}{4 \pi a}\left(I_{2}-I_{1}\right)$
$=\frac{\mu_{0}}{4 a}\left(\frac{2}{3} I-\frac{I}{3}\right)$
$=\frac{\mu_{0}}{4 a}\left(\frac{I}{3}\right)=\frac{\mu_{0} I}{12 a}$