Question

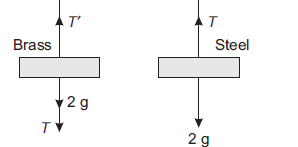
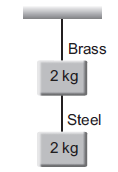
If the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are $a, b$ and $c$ respectively, the ratio between the increase in lengths of brass and steel wires would be

• A. $\frac{b^{2} a}{2 c}$
• B. $\frac{b c}{2 a^{2}}$
• C. $\frac{b a^{2}}{2 c}$
• D. $\frac{a}{2 b^{2} c}$

Answer 1

Answer: (A)

Free body diagram of the two blocks are

Given, $\frac{l_{1}}{l_{2}}=a, \frac{r_{1}}{r_{2}}=b, \frac{Y_{1}}{Y_{2}}=c$
Let Young's modulus of steel is $Y_{1}$ and of brass is $Y_{2}$
$\therefore Y_{1}=\frac{F_{1} \cdot l_{1}}{A_{1} \cdot \Delta_{1}}$ ......(i)
and $Y_{2}=\frac{F_{2} \cdot l_{2}}{A_{2} \Delta l_{2}}$ ......(ii)
Dividing Eq. (i) by Eq. (ii), we get
$\frac{Y_{1}}{Y_{2}}=\frac{\frac{F_{1} \cdot l_{1}}{A_{1} \cdot \Delta_{1}}}{\frac{F_{2} \cdot l_{2}}{A_{2} \cdot \Delta l_{2}}} $
or $\frac{Y_{1}}{Y_{2}}=\frac{F_{1} \cdot A_{2} \cdot l_{1} \cdot \Delta l_{2}}{F_{2} \cdot A_{1} \cdot l_{2} \cdot \Delta_{1}}$ ......(iii)
Force on steel wire from free body diagram
$T=F_{1}=(2 g) $ newton
Force on brass wire from free body diagram
$F_{2}=T^{\prime}=T+2 g=(4 g)$ newton
Now, putting the value of $F_{1}, F_{2}$, in Eq. (iii), we get
$\frac{Y_{1}}{Y_{2}} =\left(\frac{2 g}{4 g}\right) \cdot\left(\frac{\pi r_{2}^{2}}{\pi r_{1}^{2}}\right) \left[\frac{l_{1}}{l_{2}}\right] \cdot\left(\frac{\Delta l_{2}}{\Delta l_{1}}\right) $
OR $c =\frac{1}{2}\left(\frac{1}{b^{2}}\right) \cdot a\left(\frac{\Delta l_{2}}{\Delta_{1}}\right) $
OR $\frac{\Delta l_{1}}{\Delta l_{2}}=\left(\frac{a}{2 b^{2} c}\right) $