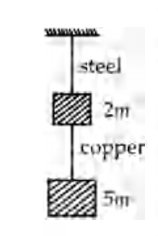
Q.
If the ratio of diameters, lengths and Young's modulus of steel and copper wires shown in the figure are $p, q$ and $s$ respectively, then the corresponding ratio of increase in their lengths would be :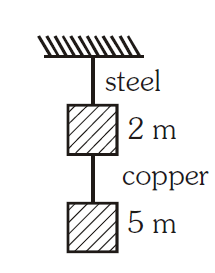
Solution:
As $ \gamma = \frac{FL}{A \Delta L} = \frac{ 4 FL}{ \pi D^2 \Delta L}$
$ \Delta L = \frac{4 FL}{ \pi D^2 \gamma}$
$\therefore \, \, \, \frac{ \Delta L_s }{ \Delta L_c} = \frac{ F_s L_s {D_c}^2 Y _c}{ F_cL_c {D_s}^2 Y_s} $
where subscripts 5 and C refer to copper and steel
respectively.
Here,
$ F_s = ( 5 m + 2 m) g = 7 mg $
$ F_c = 5 mg $
$ \frac{L_s}{L_c} = q, \frac{D_s}{D_c} = p,\frac{Y_s}{Y_c} = s$
$\therefore \, \, \, \, \, \frac{ \Delta L_s}{\Delta L_c} = \bigg(\frac{ 7 mg}{ 5 mg } \bigg) (q) \bigg( \frac{1}{p} \bigg)^2 \bigg( \frac{1}{s} \bigg) = \frac{ 7 q}{ 5 p^2 s}$