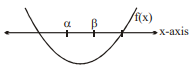
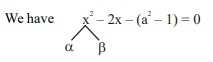Question

If the range of values of a for which the roots of the equation $x^2-2 x-a^2+1=0$ lie between the roots of the equation $x^2-2(a+1) x+a(a-1)=0$ is $(p, q)$, find the value of $\left(q+\frac{1}{p^2}\right)$.

Answer 1

$\therefore \alpha, \beta=\frac{2 \pm \sqrt{4+4\left( a ^2-1\right)}}{2}=1 \pm a$

Let $f(x)=x^2-2(a+1) x+a(a-1)$
Now, $f (\alpha)<0$ and $f (\beta)<0$ must hold simultaneously.
So,
$f (\alpha)<0 \Rightarrow a >\frac{-1}{3}$.......(1)
and
$f (\beta)<0 \Rightarrow \frac{-1}{4}< a <1$.......(2)
$\therefore$From (1) and (2), we get
$a \in\left(\frac{-1}{4}, 1\right) \Rightarrow p=\frac{-1}{4} \text { and } q=1 \Rightarrow \left(q+\frac{1}{p^2}\right)=1+16=17$