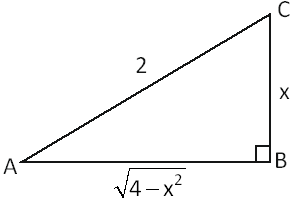
Question

If the product of height and square of the radius of the greatest cone obtained by rotating a right-angled triangle of hypotenuse $2$ meters about a side is $\frac{k}{3 \sqrt{3}}$ , then $k$ is equal to

Answer 1

Let, the cone is obtained by rotating about $BC$
From the diagram, the radius of the cone is $AB$ and the height is $BC$
The volume generated, $V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi \left(4 - x^{2}\right)\left(x\right)$
For maximum volume, $\frac{d V}{d x}=0$
$\Rightarrow 4-3x^{2}=0\Rightarrow x=\frac{2}{\sqrt{3}}$
$\therefore V_{m a x}=\frac{\pi }{3}\left(4 - \frac{4}{3}\right)\frac{2}{\sqrt{3}}=\frac{16 \pi }{9 \sqrt{3}}$
Also, $\frac{d^{2} V}{d x^{2}} < 0$
Hence, $x\left(4 - x^{2}\right)=\frac{2}{\sqrt{3}}\left(4 - \frac{4}{3}\right)=\frac{16}{3 \sqrt{3}}$