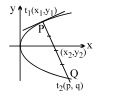
Question

If the normals to the parabola $y ^2=4 ax$ at the point $P$ meets the curve again in $Q$ and $y _1, y _2$ be the ordinates of $P$ and the middle point of $PQ$ respectively then $y _1 y _2$ is equal to

• A. $-a^2$
• B. $-2 a^2$
• C. $-4 a^2$
• D. $-8 a ^2$

Answer 1

Answer: (C)

$ t _2=- t _1-\frac{2}{ t _1} \ldots .(1) $
$\text { also } at _1^2= x _1 ; at _2^2= p ; 2 at _1= y _1 ; 2 at _2= q $
$q ^{+} y _1=2 y _2 $
$2 at _2+2 at _1=2 y _2 \Rightarrow 2 a \left( t _1+ t _2\right)=2 y _2 $
$-\frac{4 a }{ t _1}=2 y _2 \text { from (1); putting } t _1=\frac{ y _1}{2 a } \left( t _1+ t _2=-\frac{2}{ t _1}\right) $
$2 y _2=-\frac{(4 a )(2 a )}{ y _1} \therefore y _1 y _2=-4 a ^2 \Rightarrow( C )$