1. Tardigrade
  2. Question
  3. Mathematics
  4. If the maximum area of trapezium ABCD formed by points A ( x , 0), B ( x , x +(1/ x )), C (- x , e - x ), D (- x , 0) is S, where 0< x ≤ 1, then find the value of [ eS ]. [Note: [ k ] denote the greatest integer less than or equal to k and ' e ' is napier constant.]

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

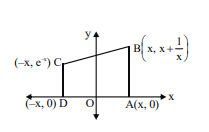
Q. If the maximum area of trapezium $ABCD$ formed by points $A ( x , 0), B \left( x , x +\frac{1}{ x }\right), C \left(- x , e ^{- x }\right)$, $D (- x , 0)$ is $S$, where $0< x \leq 1$, then find the value of $[ eS ]$.
[Note : [ $k$ ] denote the greatest integer less than or equal to $k$ and ' $e$ ' is napier constant.]

Application of Derivatives

Solution:

Area of trapezium $\Delta=1+ x ^2+ xe ^{- x }$
and $\frac{ d \Delta}{ dx } \geq 0$ when $x \in(0,1]$
$\therefore S =\Delta_{\max }=2+\frac{1}{ e }$, when $x =1$
$\therefore[ es ]=6 . $

Solution Image