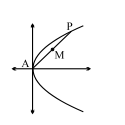
Question

If the locus of the middle points of all chords of the parabola $y^2=12 x$ passing through the vertex is the parabola $P$, then find the area bounded by the parabola $x ^2=4 y$ and $P$.

Answer 1

$P \left(3 t ^2, 6 t \right)$
Mid-point of AP
$ M \left(\frac{3}{2} t ^2, 3 t \right)= M ( h , k ) $
$\therefore k ^2=9 t ^2 $
$ h =\frac{3 t ^2}{2}=\frac{3 k ^2}{18} $
$\therefore \text { locus is } P : y ^2=6 x$
Hence area bounded by the parabola $x^2=4 y$ and $y^2=6 x$ is $16 \times(1) \times \frac{6}{4} \times \frac{1}{3}=\frac{96}{12}=8$