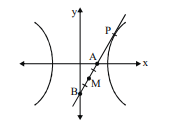
Question

If the locus of midpoints of portions of tangents intercepted between co-ordinate axes of hyperbola $\frac{x^2}{16}-\frac{y^2}{9}=1$ is $\frac{\alpha}{x^2}-\frac{9}{y^2}=\beta$, then $(\alpha+\beta)$ is equal to

• A. 14
• B. 16
• C. 18
• D. 20

Answer 1

Answer: (D)

$\frac{x^2}{16}-\frac{y^2}{9}=1$
Let point $P (4 \sec \theta, 3 \tan \theta)$
Tangent at point $P$ is given by $T=0$
$\frac{ x \sec \theta}{4}-\frac{ y \tan \theta}{3}=1$
$A =\left(\frac{4}{\sec \theta}, 0\right), B =\left(0, \frac{-3}{\tan \theta}\right)$
Let mid point of $A B$ is $M(h, k)$
$\therefore h =\frac{4}{2 \sec \theta}, k =\frac{-3}{2 \tan \theta}$
As we know, $\sec ^2 \theta-\tan ^2 \theta=1 \Rightarrow \frac{16}{4 h^2}-\frac{9}{4 k^2}=1 \Rightarrow \frac{16}{x^2}-\frac{9}{y^2}=$
Compare with $\frac{\alpha}{ x ^2}-\frac{9}{ y ^2}=\beta ; \alpha=16, \beta=4 \Rightarrow(\alpha+\beta)=20$.