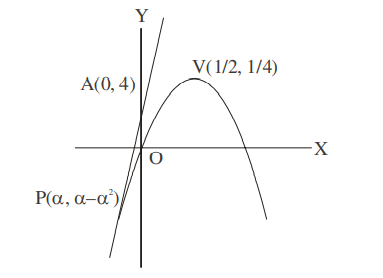
Q. If the line $y =4+ kx , k >0$, is the tangent to the parabola $y = x - x ^{2}$ at the point $P$ and $V$ is the vertex of the parabola, then the slope of the line through $P$ and $V$ is :
Solution:
Slope of tangent at $P =$ Slope of line $AP$
$\left. y ^{\prime}\right|_{ P }=1-2 \alpha=\frac{\alpha-\alpha^{2}-4}{\alpha}$
Solving $\alpha=-2 \Rightarrow P(-2,-6)$
Slope of $PV =\frac{5}{2}$