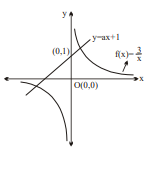
Q. If the graph of $f(x)=\frac{3}{x}$ and $g(x)=a x+1$ intersect at two distinct points then the range of a is equal to
Application of Derivatives
Solution:
Case-I: If slope of line $= a >0$ then two intersection point,
So, $ a \in(0, \infty)$....(1)
Case-II: If $a <0$
$\left.\frac{ dy }{ dx }\right|_{ P \left( a , \frac{3}{ a }\right)}=\frac{-3}{ a ^2}=\frac{\frac{3}{ a }-1}{ a -0} \Rightarrow \frac{-3}{ a ^2}=\frac{3- a }{ a ^2} \Rightarrow a =6 $
$\therefore \text { Slope at } P =\frac{-1}{12} \text { (For tangency) }$
$\therefore $ Slope at $P =\frac{-1}{12}$ (For tangency)
So, $a \in\left(\frac{-1}{12}, 0\right)$....(2)
Hence, $(1) \cup(2) \Rightarrow\left(\frac{-1}{12}, 0\right) \cup(0, \infty)$.