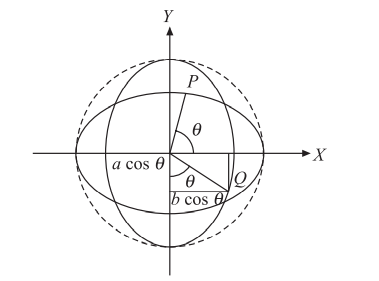
Q. If the ellipse $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ is rotated about centre in its own plane by $90^{\circ}$ in clockwise direction then the point $(a \cos \theta, b \sin \theta)$ becomes
Conic Sections
Solution:
Point $P$ goes to $Q$. Its direction with respect to $x$-axis is $q$ in original position. In new position $y$-axis will play the role of major axis so its inclination with negative direction of $y$-axis will be same. So, new coordinates will be $(b \sin \theta,-a \cos \theta)$.