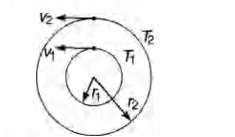
Q. If the distance between the earth and the sun were half its present value, the number of days in a year would have been
IIT JEEIIT JEE 1996Gravitation
Solution:
From Kepler's third law $T^2 \propto r^3 \, \, \, or \, \, \, \, T \propto (r)^{3/2}$
$\therefore \, \, \frac{T_2}{T_1} = \bigg( \frac{ r_2}{r_1}\bigg)^{3/2} \, \, \, \, or \, \, \, \, T_2 =T_1 \bigg( \frac{r_2}{r_1} \bigg)^{3/2} \, \, = (365) \bigg(\frac{1}{2} \bigg)^{3/2}$
$ \Rightarrow \, \, \, \, \, T_2 = 129 days $