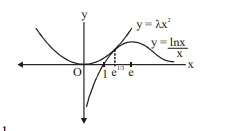
Q. If the curves $C _1: y =\frac{\ln x }{ x }$ and $C _2: y =\lambda x ^2$ (where $\lambda$ is constant) touches each other, then the value of $\lambda$ is
Application of Derivatives
Solution:
Since, $C _1$ and $C _2$ touches each other.
$\Rightarrow \frac{\ln x }{ x }=\lambda x ^2 $
$\Rightarrow \ln x =\lambda x ^3$....(1)
And $\frac{1-\ln x}{x^2}=2 \lambda x \Rightarrow 1-\lambda x^3=2 \lambda x^3$
$\Rightarrow 3 \lambda x ^3=1 \Rightarrow x =\left(\frac{1}{3 \lambda}\right)^{\frac{1}{3}}=(3 \lambda)^{\frac{-1}{3}}$
From (1), $\frac{-1}{3} \ln (3 \lambda)=\lambda \cdot \frac{1}{3 \lambda} \Rightarrow \ln (3 \lambda)=-1 . \Rightarrow \lambda=\frac{1}{3 e }$