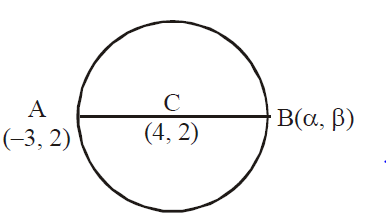
Q. If the coordinates at one end of a diameter of the circle $x^2 + y^2 - 8x - 4y + c = 0$ are $(-3, 2)$, then the coordinates at the other end are
VITEEEVITEEE 2019
Solution:
The centre of the given circle is $C \equiv (4, 2)$
Let $A \equiv (-3, 2)$
If $(\alpha, \beta)$ are the coordinates of the other end of the diameter, then, as the middle ploint of the diameter is the centre,
$\therefore \frac{\alpha-3}{2}=4$ and $\frac{\beta+2}{2}=2 \Rightarrow \alpha=11, \beta=2$
Thus, the coordinates of the other end of diameter are $(11, 2)$