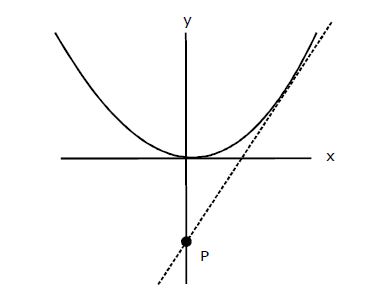
Q. If the common tangents to the parabola, $x^2 = 4y$ and the circle, $x^2 + y^2 = 4$ intersect at the point P, then the distance of P from the origin, is :
Solution:
tangent to $x^{2} + y^{2} = 4$
$y = mx \pm 2\sqrt{1+m^{2}}$
$x^{2} = 4y$
$x^{2} = 4mx + 8 \sqrt{1+m^{2}} $
$x^{2} = 4mx - 8 \sqrt{1+m^{2}} = 0$
$D = 0$
$16m^{2} + 4.8\sqrt{1+m^{2}} = 0$
$m^{2} + 2\sqrt{1+m^{2}} = 0$
or $m^{2} = \sqrt{1+m^{2}}
m^{4} = 4 + 4m^{2}$
$m^{4 }- 4m^{2} - 4 = 0$
$m^{2} = \frac{4\pm\sqrt{16+16}}{2}$
$= \frac{4\pm4\sqrt{2}}{2}$
$m^{2} = 2+2\sqrt{2}$