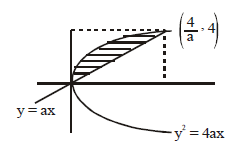
Q. If the area enclosed by $y^2 = 4ax$ and line y = ax is 1/3 sq. units , then the area enclosed by y = 4x with same parabola is
Application of Integrals
Solution:
Point of intersection of $y^2 = 4ax$
and $y =ax$ are (0,0) and $\left( \frac{4}{a} , 4 \right)$
Given $\int^4_0\left[\frac{y}{a} - \frac{y^{2}}{4a}\right] dy = \frac{1}{3}$
$ \Rightarrow \frac{8}{a} - \frac{1}{12a} \times64 = \frac{1}{3} \Rightarrow \frac{8}{3a} = \frac{1}{3} \Rightarrow a=8 $
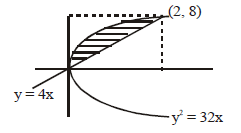
So, the parabola is $y^2 = 32x$
Area enclosed by y = 4x is
$\int^{8}_{0} \left[\frac{y}{4} - \frac{y^{2}}{32}\right]dy = \left[\frac{y^{2}}{8} - \frac{y^{3}}{96}\right]^{8}_{0} = \frac{8}{3} $