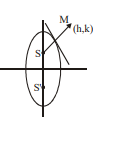
Question

If the area enclosed by the locus of image of the anyone focus of the ellipse $\frac{x^2}{9}+\frac{y^2}{25}=1$ with respect to any of the tangent to the ellipse is $k \pi$, where $k \in N$, then find sum of digits of $k$.

Answer 1

Let $M ( h , k )$ be image of focus.
$\therefore$ Mid point of line joining focus and image should lie on auxiliary circle of ellipse which is $x^2+y^2=25$ and mid point is $\left(\frac{h}{2}, \frac{k \pm 4}{2}\right)$
$\therefore \frac{ h ^2}{4}+\frac{( k \pm 4)^2}{4}=25$
$\therefore$ Locus of image is $x^2+(y \pm 4)^2=100$
$\therefore$ Image is a circle of radius $=10$
$\therefore$ Area bounded $=100 \pi$
$\therefore$ Sum of digits $=1$.