Q. If the area bounded by the curve $y=\left|\cos ^{-1}(\sin x)\right|-\left|\sin ^{-1}(\cos x)\right|$ and $x$-axis from $\frac{3 \pi}{2} \leq x \leq 2 \pi$, is equal to $\frac{\pi^2}{ k }$, where $k \in N$, then find $k$.
Application of Integrals
Solution:
We have $y=\left|\cos ^{-1}(\sin x)\right|-\left|\sin ^{-1}(\cos x)\right|=\left|\frac{\pi}{2}-\sin ^{-1}(\sin x)\right|-\left|\frac{\pi}{2}-\cos ^{-1}(\cos x)\right|$
$=\left|\frac{\pi}{2}-(x-2 \pi)\right|-\left|\frac{\pi}{2}-(2 \pi-x)\right|=\left|\frac{5 \pi}{2}-x\right|-\left|x-\frac{3 \pi}{2}\right|=\left(\frac{5 \pi}{2}-x\right)-\left(x-\frac{3 \pi}{2}\right)=4 \pi-2 x$
$\left(\right.$ For $x \in\left[\frac{3 \pi}{2}, 2 \pi\right], \sin ^{-1}(\sin x)=x-2 \pi$ and $\left.\cos ^{-1}(\cos x)=2 \pi-x\right)$
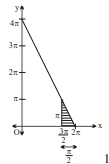
Clearly required area $=$ Area of shaded triangle in figure
$=\frac{1}{2} \times\left(\frac{\pi}{2}\right) \times \pi=\frac{\pi^2}{4}=\frac{\pi^2}{ k } \text { (Given) }$
Hence $k=4$