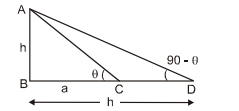
Question

If the angles of elevation of the top of a tower from two points distant $a$ and $b$ from the base and in the same straight line with it are complementary, then the height of the tower is

• A. $a b$
• B. $\sqrt{a b}$
• C. $\frac{a}{b}$
• D. $\sqrt{\frac{a}{b}}$

Answer 1

Answer: (B)

In $\triangle ABC$
$\tan \theta=\frac{h}{a}$.....(i)

$\tan (90-\theta)=\frac{ h }{ b }$
In $\triangle ABC$
$\tan (90-\theta)=\frac{ h }{ a }$
By equation (i) and (ii)
$\tan \theta \cdot \cot \theta =\frac{ h }{ a } \cdot \frac{ h }{ b } $
$\Rightarrow h ^2= ab \Rightarrow h =\sqrt{ ab }$